datawhale-pandas缺失数据处理

缺失数据

import numpy as np
import pandas as pd

一、缺失值的统计和删除

1. 缺失信息的统计

缺失数据可以使用 isna 或 isnull （两个函数没有区别）来查看每个单元格是否缺失，结合 mean 可以计算出每列缺失值的比例：

df =pd.read_csv('data/learn_pandas.csv',
               usecols=['Grade','Name','Gender','Height','Weight','Transfer'])

df.isna().head()

df.isna().mean()#查看缺失的比例

如果想要查看某一列缺失或者非缺失的行，可以利用Serires上的isna或者notna进行布尔索引，例如，查看身高缺失的行：

df[df.Height.isna()].head()

sub_set=df[['Height','Weight','Transfer']]
df[sub_set.isna().all(axis=1)]# 全部缺失

df[sub_set.isna().any(1)].head()

缺失信息的删除

数据处理中经常需要根据缺失值的大小、比例或其他特征来进行行样本或列特征的删除，pandas中提供了dropna函数来进行操作。

dropna的主要参数为轴方向axis（默认为0，即删除行），删除方式how，删除的非缺失值格式阈值thresh（非缺失值没有到达这个数量的相应维度会被删除），备选的删除子集subset，其中how主要有any和all两种参数可以选择

例如，删除身高体重至少有一个缺失的行

res=df.dropna(how='any',subset=['Height','Weight'])
res.shape

例如删除超过15个缺失值的列

res=df.dropna(axis=1,thresh=df.shape[0]-15)

res.head()

当然，不用 dropna 同样是可行的，例如上述的两个操作，也可以使用布尔索引来完成：

res=df.loc[df[['Height','Weight']].notna().all(1)]

res.shape

res=df.loc[:,~(df.isna().sum()>15)]

res.head()

二、缺失值的填充和插值

1. 利用fillna进行填充

在fillna中有三个参数是常用的：value,method,limit其中value为填充值，可以是标量，也可以是索引到元素的字典映射，method为填充方法，有用前面的元素填充ffill和用后面的元素填充bfill两种类型，limit参数表示连续缺失值的最大填充次数

下面构造一个简单的Series来说明用法

s=pd.Series([np.nan,1,np.nan,np.nan,2,np.nan],
           list('aaabcd'))

s

s.fillna(method='ffill') # 用前面的值填充

s.fillna(method='bfill')

s.fillna(method='ffill', limit=1) # 连续出现的缺失，最多填充一次

s.fillna(s.mean())# 均值填充

s.fillna({'a':100,'d':200})# 通过索引映射填充的值

有时为了更加合理地填充，需要先进行分组后再操作。例如，根据年级进行身高的均值填充：

df.groupby('Grade')['Height'].transform(
                        lambda x:x.fillna(x.mean())).head()

练一练

对一个序列以如下规则填充缺失值：如果单独出现的缺失值，就用前后均值填充，如果连续出现的缺失值就不填充，即序列[1, NaN, 3, NaN, NaN]填充后为[1, 2, 3, NaN, NaN]，请利用 fillna 函数实现。（提示：利用 limit 参数）

s = pd.Series([1,np.nan,3, np.nan, np.nan])
s1 = s.fillna(method='ffill',limit=1)
s2 = s.fillna(method='bfill',limit=1)
s = pd.Series(list(map(lambda x,y: (x+y)/2 if not np.isnan(x) and not np.isnan(y) else np.nan, s1,s2)))
s

2.插值函数

在关于 interpolate 函数的 文档 描述中，列举了许多插值法，包括了大量 Scipy 中的方法。由于很多插值方法涉及到比较复杂的数学知识，因此这里只讨论比较常用且简单的三类情况，即线性插值、最近邻插值和索引插值。

对于 interpolate 而言，除了插值方法（默认为 linear 线性插值）之外，有与 fillna 类似的两个常用参数，一个是控制方向的 limit_direction ，另一个是控制最大连续缺失值插值个数的 limit 。其中，限制插值的方向默认为 forward ，这与 fillna 的 method 中的 ffill 是类似的，若想要后向限制插值或者双向限制插值可以指定为 backward 或 both 。

s = pd.Series([np.nan, np.nan, 1,
  ....:                np.nan, np.nan, np.nan,
  ....:                2, np.nan, np.nan])
  ....:

s.values

例如，在默认线性插值法下分别进行 backward 和双向限制插值，同时限制最大连续条数为1：

res=s.interpolate(limit_direction='backward',limit=1)

res.values

res=s.interpolate(limit_direction='both',limit=1)

res.values

第二种常见的插值是最近邻插补，即缺失值的元素和离它最近的非缺失值元素一样：

s.interpolate('nearest').values

最后来介绍索引插值，即根据索引大小进行线性插值。例如，构造不等间距的索引进行演示：

s=pd.Series([0,np.nan,10],index=[0,1,10])

s

s.interpolate()#默认的线性插值，等价于计算中点的值

s.interpolate(method='index')#和索引有关的线性插值，计算相应的索引对应的值

同时，这种方法对于时间戳索引也是可以使用的，有关时间序列的其他话题会在第十章进行讨论，这里举一个简单的例子：

s=pd.Series([0,np.nan,10],
           index=pd.to_datetime(['20200101',
                                '20200102',
                                '20200111']))

s

s.interpolate()

s.interpolate(method='index')

关于polynomial和spline插值的注意事项

在 interpolate 中如果选用 polynomial 的插值方法，它内部调用的是 scipy.interpolate.interp1d(*,*,kind=order) ，这个函数内部调用的是 make_interp_spline 方法，因此其实是样条插值而不是类似于 numpy 中的 polyfit 多项式拟合插值；而当选用 spline 方法时， pandas 调用的是 scipy.interpolate.UnivariateSpline 而不是普通的样条插值。这一部分的文档描述比较混乱，而且这种参数的设计也是不合理的，当使用这两类插值方法时，用户一定要小心谨慎地根据自己的实际需求选取恰当的插值方法。

Nullable类型

1. 缺失记号及其缺陷

在 python 中的缺失值用 None 表示，该元素除了等于自己本身之外，与其他任何元素不相等：

None==None

True

None==False

False

None==[]

False

None==''

False

在 numpy 中利用 np.nan 来表示缺失值，该元素除了不和其他任何元素相等之外，和自身的比较结果也返回 False ：

np.nan==np.nan

False

np.nan==None

False

np.nan==False

False

值得注意的是，虽然在对缺失序列或表格的元素进行比较操作的时候， np.nan 的对应位置会返回 False
但是在使用 equals 函数进行两张表或两个序列的相同性检验时，会自动跳过两侧表都是缺失值的位置，直接返回 True :

s1=pd.Series([1,np.nan])

s2=pd.Series([1,2])

s3=pd.Series([1,np.nan])

s1==1

0     True
1    False
dtype: bool

s1.equals(s2)

False

s1.equals(s3)

True

在时间序列的对象中， pandas 利用 pd.NaT 来指代缺失值，它的作用和 np.nan 是一致的（时间序列的对象和构造将在第十章讨论）：

pd.to_timedelta(['30s',np.nan])#Timedelta 中的NaT

TimedeltaIndex(['0 days 00:00:30', NaT], dtype='timedelta64[ns]', freq=None)

pd.to_datetime(['20200101',np.nan])#Datetime中的NaT

DatetimeIndex(['2020-01-01', 'NaT'], dtype='datetime64[ns]', freq=None)

那么为什么要引入 pd.NaT 来表示时间对象中的缺失呢？仍然以 np.nan 的形式存放会有什么问题？在 pandas 中可以看到 object 类型的对象，而 object 是一种混杂对象类型，如果出现了多个类型的元素同时存储在 Series 中，它的类型就会变成 object 。例如，同时存放整数和字符串的列表：

pd.Series([1,'two'])

0      1
1    two
dtype: object

NaT 问题的根源来自于 np.nan 的本身是一种浮点类型，而如果浮点和时间类型混合存储，如果不设计新的内置缺失类型来处理，就会变成含糊不清的 object 类型，这显然是不希望看到的

同时，由于 np.nan 的浮点性质，如果在一个整数的 Series 中出现缺失，那么其类型会转变为 float64 ；

pd.Series([1,np.nan]).dtype

dtype('float64')

而如果在一个布尔类型的序列中出现缺失，那么其类型就会转为 object 而不是 bool ：

pd.Series([True,False,np.nan]).dtype

dtype('O')

因此，在进入 1.0.0 版本后， pandas 尝试设计了一种新的缺失类型 pd.NA 以及三种 Nullable 序列类型来应对这些缺陷，它们分别是 Int, boolean 和 string 。

2. Nullable类型的性质

从字面意义上看 Nullable 就是可空的，言下之意就是序列类型不受缺失值的影响。例如，在上述三个 Nullable 类型中存储缺失值，都会转为 pandas 内置的 pd.NA ：

pd.Series([np.nan,1],dtype='Int64')

pd.Series([np.nan,True],dtype='boolean')

pd.Series([np.nan,'my_str'],dtype='string')

在 Int 的序列中，返回的结果会尽可能地成为 Nullable 的类型：

pd.Series([np.nan,0],dtype='Int64')+1

pd.Series([np.nan,0],dtype='Int64')==0

pd.Series([np.nan,0],dtype='Int64')*0.5

对于boolean类型的序列而言，其和 bool 序列的行为主要有两点区别：

第一点是带有缺失的布尔列表无法进行索引器中的选择，而 boolean 会把缺失值看作 False ：

s=pd.Series(['a','b'])

s_bool=pd.Series([True,np.nan])

s_boolean=pd.Series([True,np.nan]).astype('boolean')

s[s_bool] #报错

s[s_boolean]

第二点是在进行逻辑运算时， bool 类型在缺失处返回的永远是 False ，而 boolean 会根据逻辑运算是否能确定唯一结果来返回相应的值。
那什么叫能否确定唯一结果呢？
举个简单例子：

• True | pd.NA 中无论缺失值为什么值，必然返回 True
• False | pd.NA 中的结果会根据缺失值取值的不同而变化，此时返回 pd.NA
• False & pd.NA 中无论缺失值为什么值，必然返回 False 。

s_boolean & True

s_boolean | True

~s_boolean# 取反操作同样是无法唯一地判断缺失结果

关于 string 类型的具体性质将在下一章文本数据中进行讨论。
一般在实际数据处理时，可以在数据集读入后，先通过 convert_dtypes 转为 Nullable 类型：

df = pd.read_csv('data/learn_pandas.csv')

df=df.convert_dtypes()

df.dtypes

3. 缺失数据的计算和分组

当调用函数sum,prod使用加法和乘法的时候，缺失数据等价于被分别视作0和1，即不改变原来的计算结果

s=pd.Series([2,3,np.nan,4,5])

s.sum(),s.prod()

当使用累计函数的时候，会自动跳过缺失值所处的位置

s.cumsum()

当进行单个标量运算的时候，除了 np.nan ** 0 和 1 ** np.nan 这两种情况为确定的值之外，所有运算结果全为缺失（ pd.NA 的行为与此一致 ），并且 np.nan 在比较操作时一定返回 False ，而 pd.NA 返回 pd.NA

np.nan==0

pd.NA==0

np.nan>0

pd.NA>0

np.nan+1

np.log(np.nan)

np.add(np.nan,1)

np.nan**0

pd.NA**0

1**np.nan

1**pd.NA

s.diff()

s.pct_change()

对于一些函数而言，缺失可以作为一个类别处理，例如在 groupby, get_dummies 中可以设置相应的参数来进行增加缺失类别:

df_nan=pd.DataFrame({'category':['a','a','b',np.nan,np.nan],
                    'value':[1,3,5,7,9]})

df_nan

df_nan.groupby('category',dropna=False)['value'].mean()

pd.get_dummies(df_nan.category,dummy_na=True)

Ex1：缺失值与类别的相关性检验

在数据处理中，含有过多缺失值的列往往会被删除，除非缺失情况与标签强相关。下面有一份关于二分类问题的数据集，其中 X_1, X_2 为特征变量， y 为二分类标签

df=pd.read_csv('data/missing_chi.csv')

df.head()

df.isna().mean()

df.y.value_counts(normalize=True)

事实上，有时缺失值出现或者不出现本身就是一种特征，并且在一些场合下可能与标签的正负是相关的。关于缺失出现与否和标签的正负性，在统计学中可以利用卡方检验来断言它们是否存在相关性。

按照特征缺失的正例、特征缺失的负例、特征不缺失的正例、特征不缺失的负例，可以分为四种情况，设它们分别对应的样例数为 n11,n10,n01,n00 。

假若它们是不相关的，那么特征缺失中正例的理论值，就应该接近于特征缺失总数 × 总体正例的比例，即：

$$ E_{11} = n_{11} \approx (n_{11}+n_{10}) \times \frac{n_{11}+n_{01}}{n_{11}+n_{10}+n_{01}+n_{00}} = F_{11}$$

其他的三种情况同理，现将实际值和理论值分别记作$E_{ij},F_{ij}$,那么希望下面的统计量越小越好，即代表实际值接近不相关情况的理论值：

$$S = \sum_{i \in { 0,1} } \sum_{ j \in {0,1}} \frac{(E_{ij} - F_{ij})^2}{F_{ij}} $$

可以证明上面的统计量近似服从自由度为 1 的卡方分布，即$S\overset{\cdot}{\sim} \chi^2(1) $因此，可通过计算 $P(\chi^2(1)>S)$的概率来进行相关性的判别，一般认为当此概率小于 0.05 时缺失情况与标签正负存在相关关系，即不相关条件下的理论值与实际值相差较大。

上面所说的概率即为统计学上关于 $2\times 2 $列联表检验问题的 p 值， 它可以通过 scipy.stats.chi2.sf(S, 1) 得到。请根据上面的材料，分别对 X_1, X_2 列进行检验。

df=pd.read_csv('data/missing_chi.csv')

cat_1 = df.X_1.fillna('NaN').mask(df.X_1.notna()).fillna("NotNaN")
cat_2 = df.X_2.fillna('NaN').mask(df.X_2.notna()).fillna("NotNaN")

交叉表(crossTab)
交叉表是用于统计分组频率的特殊透视表

df_1 = pd.crosstab(cat_1, df.y, margins=True)
df_2 = pd.crosstab(cat_2, df.y, margins=True)

def compute_S(my_df):
    S = []
    for i in range(2):
        for j in range(2):
            E = my_df.iat[i, j]
            F = my_df.iat[i, 2]*my_df.iat[2, j]/my_df.iat[2,2]
            S.append((E-F)**2/F)
    return sum(S)

res1 = compute_S(df_1)
res2 = compute_S(df_2)
from scipy.stats import chi2
chi2.sf(res1, 1) # X_1检验的p值 # 不能认为相关，剔除

chi2.sf(res2,1)

Ex2：用回归模型解决分类问题

KNN 是一种监督式学习模型，既可以解决回归问题，又可以解决分类问题。对于分类变量，利用 KNN 分类模型可以实现其缺失值的插补，思路是度量缺失样本的特征与所有其他样本特征的距离，当给定了模型参数 n_neighbors=n 时，计算离该样本距离最近的 n 个样本点中最多的那个类别，并把这个类别作为该样本的缺失预测类别，具体如下图所示，未知的类别被预测为黄色：

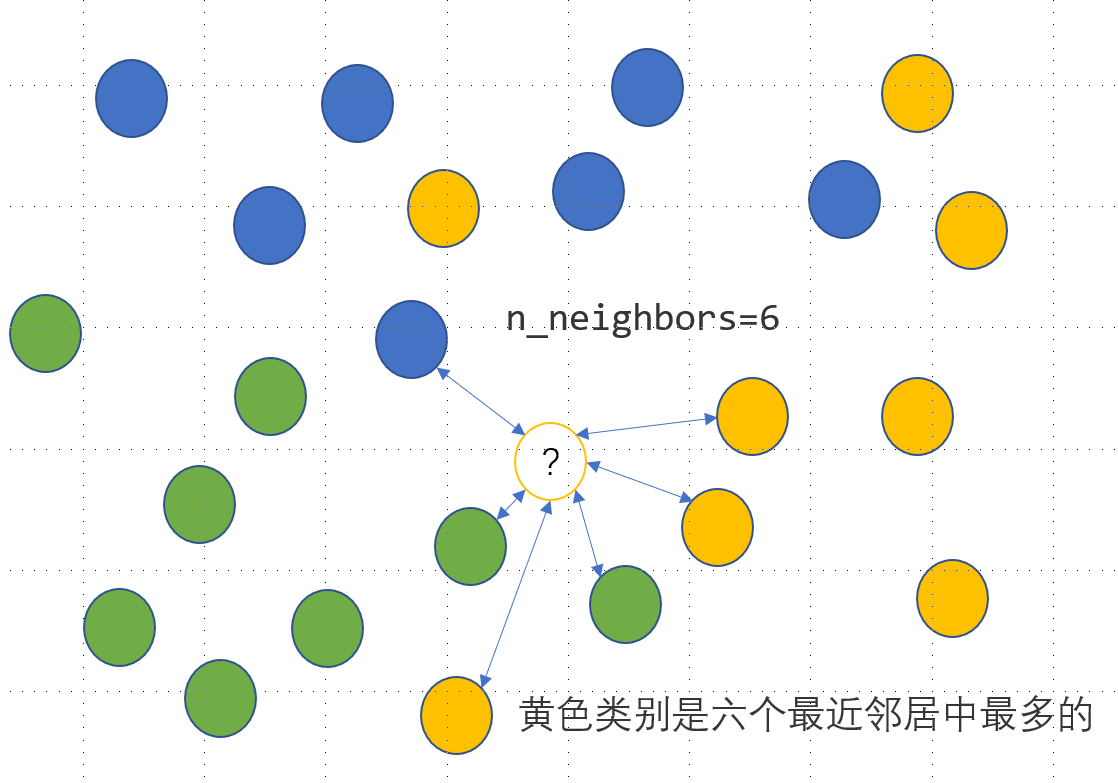
上面有色点的特征数据提供如下：

df=pd.read_excel('data/color.xlsx')

df.head(3)

已知待预测的样本点为 $X_1=0.8,X_2=−0.2$ ，那么预测类别可以如下写出

from sklearn.neighbors import KNeighborsClassifier

clf=KNeighborsClassifier(n_neighbors=6)

clf.fit(df.iloc[:,:2],df.Color)

clf.predict([[0.8,-0.2]])

1.对于回归问题而言，需要得到的是一个具体的数值，因此预测值由最近的 n 个样本对应的平均值获得。请把上面的这个分类问题转化为回归问题，仅使用 KNeighborsRegressor 来完成上述的 KNeighborsClassifier 功能。

标准答案

from sklearn.neighbors import KNeighborsRegressor
df = pd.read_excel('../data/color.xlsx')
df_dummies = pd.get_dummies(df.Color)
stack_list = []
for col in df_dummies.columns:
    clf = KNeighborsRegressor(n_neighbors=6)
    clf.fit(df.iloc[:,:2], df_dummies[col])
    res = clf.predict([[0.8, -0.2]]).reshape(-1,1)
    stack_list.append(res)
code_res = pd.Series(np.hstack(stack_list).argmax(1))
df_dummies.columns[code_res[0]]

from sklearn.neighbors import KNeighborsRegressor
df=pd.read_excel('data/color.xlsx')
df_dummies=pd.get_dummies(df.Color)

df_dummies.head()#转换成one-hot编码模式

stack_list = []
for col in df_dummies.columns:
    print(col)
    clf = KNeighborsRegressor(n_neighbors=6)
    clf.fit(df.iloc[:,:2], df_dummies[col])
    res = clf.predict([[0.8, -0.2]]).reshape(-1,1)
    print(res)
    stack_list.append(res)

np.hstack(stack_list).argmax(1)

code_res = pd.Series(np.hstack(stack_list).argmax(1))
df_dummies.columns[code_res[0]]

2.请根据第1问中的方法，对 audit 数据集中的 Employment 变量进行缺失值插补。

df = pd.read_csv('data/audit.csv')
pd.get_dummies(df[['Marital', 'Gender']])

from sklearn.neighbors import KNeighborsRegressor
df = pd.read_csv('data/audit.csv')
res_df = df.copy()
res_df2 = df.copy()
#数据处理加归一化这句写的很妙
df = pd.concat([pd.get_dummies(df[['Marital', 'Gender']]), df[['Age','Income','Hours']].apply(lambda x:(x-x.min())/(x.max()-x.min())), df.Employment],1)
df.head()

使用KNN分类法

from sklearn.neighbors import KNeighborsClassifier
clf=KNeighborsClassifier(n_neighbors=6)
train=df[df.Employment.notna()]
test=df[df.Employment.isna()]
clf.fit(train.iloc[:,:-1],train.Employment)
predict=clf.predict(test.iloc[:,:-1])
res_df2.loc[res_df.Employment.isna(), 'Employment'] = predict
res_df2.isna().sum()

使用KNN分类树

X_train = df[df.Employment.notna()]
X_test = df[df.Employment.isna()]
df_dummies = pd.get_dummies(X_train.Employment)
stack_list = []
for col in df_dummies.columns:
    clf = KNeighborsRegressor(n_neighbors=6)
    clf.fit(X_train.iloc[:,:-1], df_dummies[col])
    res = clf.predict(X_test.iloc[:,:-1]).reshape(-1,1)
    stack_list.append(res)
code_res = pd.Series(np.hstack(stack_list).argmax(1))
cat_res = code_res.replace(dict(zip(list(range(df_dummies.shape[0])),df_dummies.columns)))
res_df.loc[res_df.Employment.isna(), 'Employment'] = cat_res.values
res_df.isna().sum()